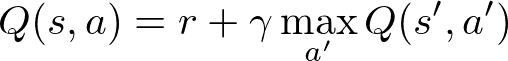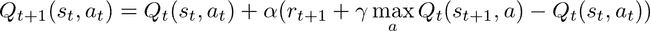Applying Deep Reinforcement Learning to Poker

We will cover the subject of Deep Reinforcement Learning, more specifically the Deep Q Learning algorithm introduced by DeepMind, and then we’ll apply a version of this algorithm to the game of Poker.

Reinforcement learning

Machine Learning and Deep Learning have become a hot topic in the past years. With the recent improvements in parallel computing, we have witnessed in the last decades some major breakthroughs. Algorithms are consistently solving very complex tasks such as Image/Video recognition and generation. These algorithms generally require huge datasets to achieve reasonable performances.

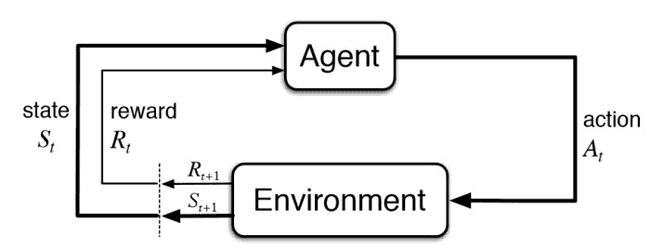
Reinforcement Learning is a type of Machine Learning where an algorithm doesn’t have training data at the beginning. The goal is for an agent to evolve in an environment and learn from its own experience. In order for a Reinforcement Learning algorithm to work, the environment (state based on actions taken) must be computable and have some kind of a reward function that evaluates how good an agent is. This is why it can be easily applied to games, as the states are clearly defined by the program, the rules are generally simple, and there is a clear goal (generally a score metric). However, Reinforcement Learning can also be applied to simulate real-world problems like robotics simulation.

A simple representation of a Reinforcement Learning algorithm.

In 2013, the startup DeepMind published a paper on Playing Atari with Deep Reinforcement Learning. The researchers at DeepMind managed to create an algorithm that could outperform top players on numerous games of Atari, using the same Neural Network architecture. It was seen as the first step to general-purpose algorithms. They introduced methods to solve common problems encountered while dealing with Reinforcement Learning.

Q learning

Q table

The main element of the Q learning algorithm is the state/action table. It is a 2-dimensional matrix, that maps a state with its corresponding values Q(s,a) for each action taken.

A representation of a Q-table, for 5 possible states and 5 possible actions.

The objective of the algorithm is to iteratively find the optimal Q-table, which maps the states to their correct Q-values. For this, we have to make use of the Bellman equation:

This equation states that the Q-value for a state and action is equal to the immediate reward plus the discounted future reward, with γ being the discount factor. Our algorithm will try to choose an action that maximizes this function, taking into account future rewards for the agent.

Using the Bellman equation, we can get the Q learning function, which enables us to update Q-values after performing an action. It includes a learning parameter α, to have a better influence on the updating of Q-values.

The general algorithm of Q learning is as follow:

Initialize Q-table randomly

Repeat until Q-table converges:
  Chose action ( maxQ(s,a) ) from Q table, given the current state
  Perform action
  Get the reward
  Update Q-table following the Q learning function

Exploitation vs Exploration

Because the Q-learning algorithm is a greedy algorithm, it will always choose the action that yields the best Q-value for the current network. However, the different Q-values are randomly generated at the beginning so the algorithm can think that bad actions will get the most reward. That is why we need to integrate a random parameter, which will make the agent choose its action randomly for a certain percent of the time. We can also decrease this chance over time to make the algorithm converge to the optimal function Q.

The aim of Q learning is to have a sort of “cheat sheet”. For each possible state, we compute the Q-value of each action. The algorithm can then choose the best possible action for each state of the environment.

However, when the environment becomes highly dimensional, such as in poker where there can be a huge number of possible states, Q-learning becomes impracticable. That’s why Deep Q Learning was introduced.

Deep Q learning

Deep Q Learning is the algorithm introduced by the DeepMind paper in 2013. It is basically an extension of the traditional Q Learning algorithm that uses a Neural network in order to approximate the Q value, given a state. This enables the algorithm to scale to complex environments and states, such as games. The number of states given by the environment doesn’t have to be predefined.

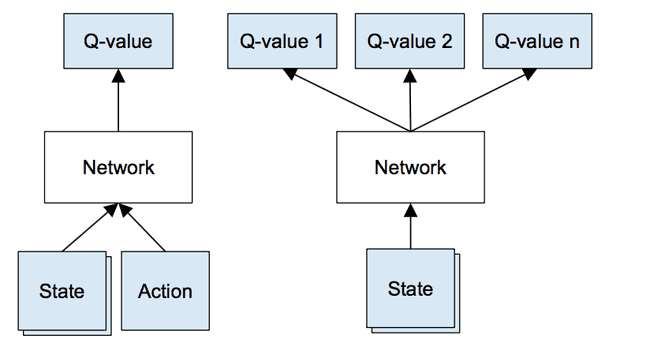
Instead of having a Q-matrix that stores every possible state and actions we use a Q-network, which is basically a neural network. It takes the state of the environment as input and outputs the predicted Q-value of each action.

The game of Poker

Poker, as opposed to Go or Chess, is a game of incomplete information. It means that each player knows only a portion of the game’s present state and the actors must infer some of these pieces of information based on other’s actions.

One of the complex aspects of Poker is the variance. Because it is partly based on luck or more precisely probabilities, a favorite drawing at a certain point in a hand can lose the game.

Even after playing thousands of hands, a player cannot be absolutely sure that his current win rate is representative of his “true” win rate. The only solution to ease out the variance is to actually play a very large number of hands that will average the spots over time. However, there are types of game where the variance is so high that nobody could ever have an idea of a true win rate. For example in big tournaments, winning the first place is often considered as winning the lottery.

Thanks to its relation with making/losing money, Poker became one of the most competitive games ever. Since the beginning of on-line games, in the 2000s, the average level increased significantly, and the top players currently make near-perfect decisions. The ability to play on computers enabled people to play many times faster than live play. With the increased volume per player came a lot of analytical tools. These tools, called trackers, can record all the hands played by a player and aggregate statistics. This allows people to find their own strengths and weaknesses. They also compute statistics for other players, which is really helpful for finding how to exploit opponents on a table.

More recently, some more theoretical tools emerged. These expensive tools often claim to play a perfect game. Some of them are marketed as Reinforcement Learning algorithms, others just brute-force each situation’s game tree to find the optimal play in each spot.

Head’s up push-or-fold

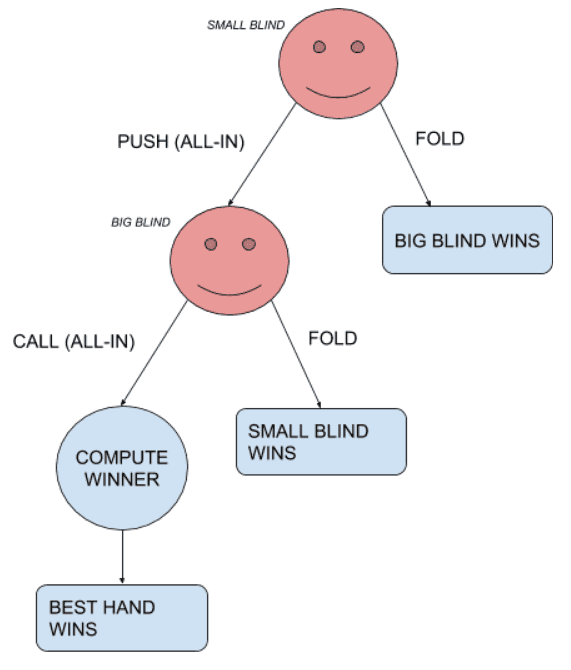
The game of Poker has many variants. One of the simplest settings is the head’s up push-or-fold scenario, in no-limit Texas Hold’em Poker. In this scenario, there are only two players. The Small Blind (first player to act) has only two actions possible: folding, thus losing the current hand, or going all-in, risking all his chips. Once the small blind went all-in, the Big Blind (second player to act) has also two actions possible: folding, meaning he lost the hand or calling the small blind’s all-in. Once the two players went all-in, the 5 community cards are dealt, and the best hand wins the pot.

A representation of the situation.

If no money was involved before taking a decision, the optimal strategy for this situation would be for the two players to always fold, and to only go all-in when holding the best hand possible (a pair of Aces, once every 221 hands dealt). However, each player has already put some chips, the blinds. If a player only played with Aces, he would slowly lose money over time against a more aggressive player. The idea in this situation is to find a sort of equilibrium.

The definition of a Nash equilibrium is a proposed solution of a non-cooperative game involving two or more players in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only their own strategy.

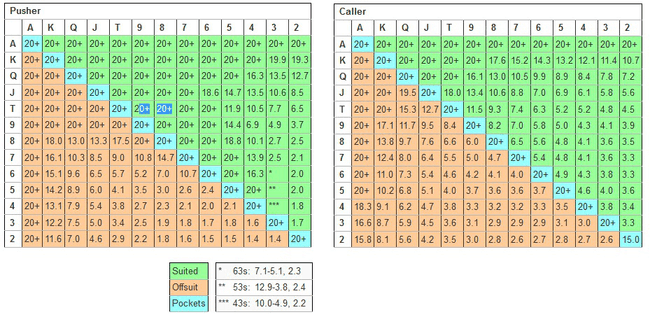
Fortunately, the Nash equilibrium has already been computed for this exact scenario. This chart represents the minimum stack, or chip count, required (in number of big blinds) for each player to push (go all-in) or call.

The optimal push-or-fold charts.

A naive thinking would be that the two charts should be equal. However looking quickly at it, we can see that the Pusher’s range is much wider than the Caller’s one. Indeed, the chart indicates that you can shove with 5-6 suited at any stack size, while the caller can only call this hand with a stack size lower than 4.6 Big Blinds.

Modeling the algorithm

Our goal is to approximate the Nash equilibrium using Deep Q Learning.

Fortunately, this situation is very easy, so we can greatly simplify the algorithm: the reward will always be immediate which means there is no need to implement future rewards in this scenario, so no discount factor. Using the Bellman Equation, we can simplify the Q-learning equation to: Qt+1(s,a) = Qt(s,a) * α[ r - Qt(s,a) ]

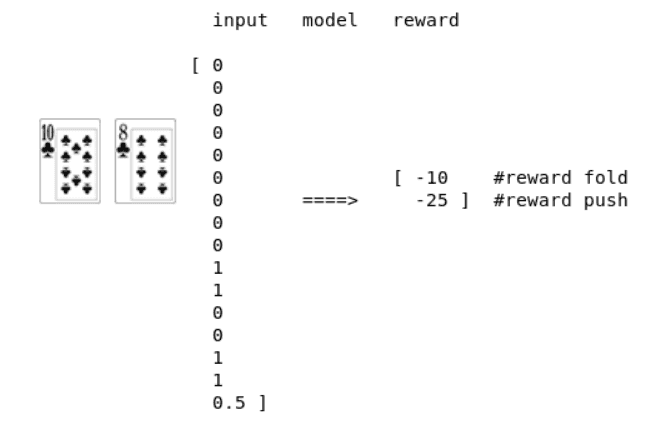
To model the state of the game, we have to encode 4 features:

• the player’s starting hand
• is the starting hand suited
• the player’s position
• the starting stack

We encode the starting hand as a one-hot encoded vector. The output of the model will be an approximation of the reward for the two possible actions.

A representation of the inputs and outputs of the model.

The actual model is a simple multi-layers fully connected neural network.

We use the Keras functional API to make a 5-layers neural network:

def preflop_model():

    input_n = Input(shape=(16,), name="input")

    x = Dense(32, activation='relu')(input_n)
    x = Dense(64, activation='relu')(x)
    x = Dense(16, activation='relu')(x)
    out = Dense(2)(x)
    model = Model(inputs=[input_n], outputs=out)
    model.compile(optimizer='adam', loss='mse')

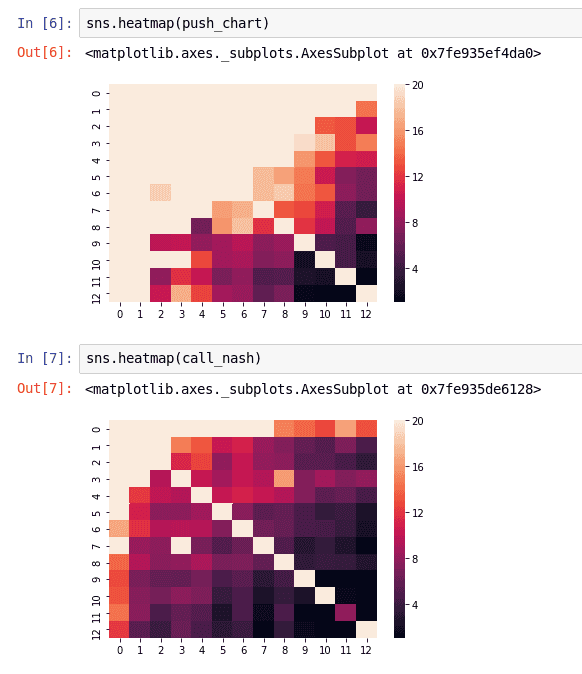
    return model

To visualize our algorithm, we feed every possible hand in the network with different stack sizes to determine the threshold between going all-in and folding. We then map these values into a matrix to obtain a heat map similar to the reference charts seen earlier:

The push and call ranges generated by our model.

After a few tens of thousands of iterations, the model seems to converge. We can see that the model has a general idea of how to play correctly in push or fold situation, the small-blind being wider than the big blind’s one. However, the results are often extreme, meaning that a lot of hands will go all-in with any stack size while others will always fold.

The full notebook is available on GitHub at this address.

Conclusion

This implementation of a Deep Q Learning algorithm is very simple. The fact that it does not take into accounts the future rewards makes using the Q-learning algorithm less interesting, and we cannot yet beat real-world players at any game of poker. A second article will cover the implementation of this algorithm on a full game of poker, with more decisions, and implementing experience replay sampling.

All the code used, as well as the poker engine made for this experimentation, is available on GitHub. A standalone project containing the two player engines can be found at this address (in progress).